
La Marge Statique
La stabilité de la fusée dépendra de sa marge statique . Celle-ci
variera au cours du vol, quand le réservoir se videra de son eau.
Mais là où elle est la plus cruciale, et la plus délicate à réaliser
sera au début du vol, réservoir plein.
Elle devra avoir une valeur comprise entre 1 & 1,5. Si la valeur est
trop faible, il y aura instabilité. Si elle est trop élevée elle sera
surstable et sensible au vent.
Calcul de la marge statique
Des logiciels trouvés sur Planète-Sciences. Voir sur leur site :
http://www.planete-sciences.org/espace/Ressources/Trajectoire/
Ou alors en téléchargement depuis ma base de données mais sans garantie:
- Trajec 2.5
|
- Carina Je ne sais si ça marche encore mais jadis...... |
Un document de Bernard de Gomars : la
stabilité intuitive
Mesure au camescope
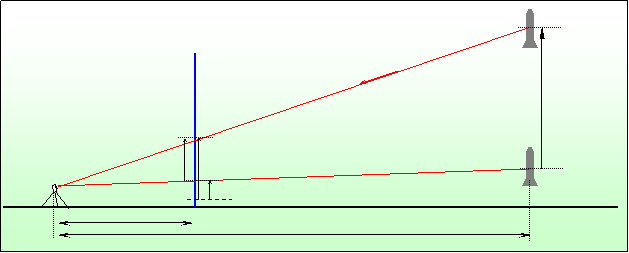
c'est la méthode que j'utilisais avant de posséder un altimètre.
L'approximation est importante, et l'erreur d'autant plus grande que la
fusée à une trajectoire éloignée de la verticale.
Il suffit de : trouver un piquet adéquat un poteau électrique
existant par exemple, ajuster la ou les distances du piquet au caméscope
et à la fusée, et de placer le caméscope sur un pied
Mesure au théodolite
Un article de Alain Juge tiré
de son site . Il
est plus intéressant d'aller voir sur son site , pour ne manquer aucune
précision
.Mesure de l'altitude
Le fusil trigonométrique
 |
 |
 |
| Le
moyen le plus simple, même s'il n'offre pas une grande précision de
mesure, est le 'fusil trigonométrique', basé sur le principe suivant : Connaissant la distance d à laquelle l'observateur se trouve du lanceur, on en déduit la hauteur h par la relation h = d*tg( alpha ). Plus l'angle est petit, meilleur est la précision, aussi il faut se placer assez loin du lanceur. Une bonne distance me semble être entre 50 et 100m . |
Mais cette méthode a des limites. D'abord la visée est plus ou moins précise, de même que l'estimation de l'apogée. Ensuite le blocage du fil à plomb avec un doigt ne va pas dans le sens de la précision. Enfin et surtout, si on considère la figure ci-contre, on se rend vite compte que si la fusée n'a pas une trajectoire dans un plan perpendiculaire à l'axe Lanceur-Observateur (cas des Fusées 2 et 3) le calcul est complètement erronée. |
Pour pallier ce problème, il faut avoir 2 observateurs et utiliser un
matériel légèrement plus sophistiqué en ce sens que chaque observateur
doit relever l'angle alpha comme précédemment, mais aussi l'angle Thêta
représenté sur la figure ci dessous.
L'altitude h est donnée par l'une des formules suivantes : h = (Yp/sin(Théta1))*tg(alpha1) |
Vous avez intérêt a rentrer ces formules dans un tableur ou dans une
calculette programmable pour avoir un résultat rapide.
Vous pouvez aussi noter soigneusement les différents angles puis faire
une construction géométrique à l'échelle 1/1000 ème par exemple (1cm=
10m).
On recherche les coordonnées de P en traçant d'abord les droite LO1 et
LO2, puis, connaissant les angles Théta1 et théta2, les droites O1P et
O2P.
Sur une autre figure, on retrace O1P et sa perpendiculaire en P, puis
connaissant l'angle alpha1, on trace la droite O1A. Pour controle, on
trace O2P et sa perpendiculaire en P et connaissant l'angle alpha2 on
trace O2A. Dans les deux cas de figure, la hauteur PA doit être la même
(aux erreurs de mesure près et aux incertitudes de construction près).
| Le premier fusil trigonométrique que j'ai (c'est Alain Juges qui parle) confectionné est constitué d'un bout de manche à balai, sous lequel j'ai collé un morceau de carton. Sur le carton, j'ai tracé un quart de cercle gradué tout les 5°. Au centre du quart de cercle, j'ai fixé une tige métallique qui est lestée de plomb à son autre extrémité.Le manche à balai permet de viser la fusée, et lors de son apogée, il faut bloquer la tige métallique (avec un doigt) pour lire l'angle alpha que fait le fusil avec l'horizontale. |
 |
Voici, ci dessous, la nouvelle version qui ressemble beaucoup plus à un
fusil. Le système de visée est donc un peu plus précis.
La mesure d'angle est réalisée grâce à un disque gradué tous les 5 degrés. Ce disque est lesté de plomb. Lorsque la fusée atteint son apogée, il suffit de bloquer le disque à l'aide de la gâchette, puis de lire l'angle en face du repère sur la partie fixe du fusil. Encore amélioré, avec la camera fixée dessus, on filme en même temps que l'on mesure l'altitude
 |
 |
 |
Avimeca
AVIMECA est un logiciel gratuit et léger permettant d'effectuer des
pointages sur les fichiers vidéo AVI.
avimeca2.zip (405ko) ensemble compacté, contenant les fichiers
avimeca2.exe (éxécutable) & avimeca2.hlp (aide)
mesam2_7.pdf (50ko) mode d'emploi simplifié

La martingale balistique de
Bernard de Gomars
Description :
Méthode de détermination de différents paramètres (l’Altitude de
Culmination, la Vitesse de Fin de Propulsion, la Distance Balistique)
par le relevé de seulement deux durées pendant le vol balistique d’une
fusée.
(La Distance Balistique est l’inverse du coefficient balistique b
utilisé, par exemple, dans le Vol de la Fusée de Gil Denis :
On a donc Distance balistique = 1/b = 2M/ρ S Cx )
Aux hydrofuséistes qui désirent un abaque d’évaluation de l’altitude de
culmination des Fusées à eau « plein goulot » de 1,5L, nous proposons
l’abaque suivant. Il y est posé que la propulsion s’étend sur 1/10ème de
seconde et sur 3m d’altitude (deux paramètres qui, de fait, sont usuels
pour ce type de Fusées).
Abscisses et ordonnées de cet abaque sont :
- le TRaS (Temps de Retour au Sol), durée totale du vol, depuis
l’instant de libération de la fusée jusqu’à son crash final.
- l’Écart Sommital, différence entre le Temps de Culmination (à savoir
le temps que met la fusée à s’élever depuis le sol jusqu’à son apogée)
et la moitié du TRaS.

–Les courbes rouges quasi verticales représentent les Hauteurs de
Culmination de valeurs rondes (30m, 35m, 40m). Les bulles rouges
précisent ces valeurs rondes pour la moitié des courbes.
–En violet sont les courbes de Vitesses de Fin de Propulsion, repérées
également pour la moitié d’entre elles.
–L’éventail de courbe de couleurs variées représente toujours les
différentes Distances Balistiques .(DB = 35m, DB = 45m, etc…)…
–Le tracé jaune reproduit, pour exemple, le vol d’une fusée type de 75m
de Distance Balistique, qui serait animée en Fin de Propulsion d’une
vitesse de 55 m/s.
–Les pointillés gris verticaux représentent le pronostic d’altitude que
l’on peut émettre à partir de la formule simplifiée de Dean Wheeler à
savoir : Zap = 1,23 TRaS² – 0,5(HfinProp+3)
(pour simplifier, seules les altitudes de 50 et 100m sont indiquées
Soulignons que cet abaque vaut pour tout les projectiles dont on peut
prétendre qu’ils sont caractérisés par un seul et unique S.Cx , càd
toutes formes de Fusées à eau (par exemple les Fusées mues par une
tuyère réduite, ou de volume plus important) ainsi que pour les Fusées à
feu.
Extrait de Le
Vol Balistique de la Fusée, par Bernard Bertin.( son
site )
Formule simplifiée de Dean Wheeler
Une infos d'Amstrong
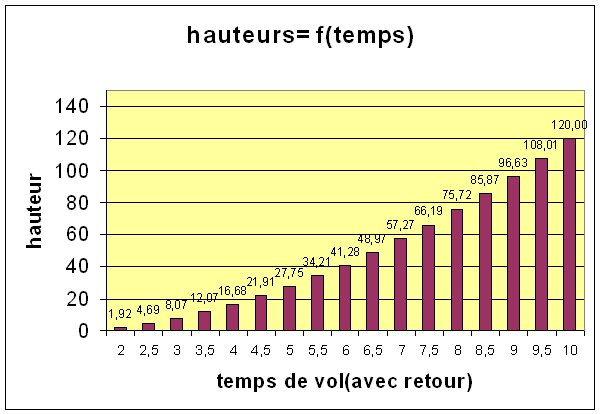
H = 1,23 T² -3
H représente la hauteur, en mètres et T le temps que met la bouteille en
vol, sans parachute (à partir du moment où elle quitte le lanceur,
jusqu'au moment où elle touche le sol)
Et un graphe de Fred
Simulation par tableau Excel
J'ai trouvé sur la toile plusieurs tableaux de simulation, celui que
j'utilise après l'avoir un peu modifié est celui-ci :
Il nécessite Excel

Télécharger : simulation trajectoire.xls (527ko)
Un autre tableau, celui de "Zorg" :

Télécharger : simulation.xls (798 ko)
Un autre simulateur : sur Polyplex.org http://polyplex.org/rockets/simulation/






